最近看了《大话数据结构》 这本书,补了补自己在这方面知识不够系统的欠缺,里面的概念还是挺多的。我尝试着以思维导图加说明的方式,来梳理一遍我所掌握的各种数据结构,希望能给大家带来一个更直观的认识。
数据结构是相互之间存在一种或多种特定关系的数据元素的集合,它是一门研究非数值计算的程序设计问题中的操作对象,以及它们之间的关系和操作等相关问题的学科。
算法
算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
为什么要在数据结构中提算法呢,因为 程序设计 = 数据结构 + 算法,它俩是不能割裂的。之所以要设计不同的数据结构,是因为各个数据结构在解决不同的问题时,有各自的优缺点,而通过算法能更科学的反应它们的优缺点。这里先简单给出一些必要的算法概念,更详细的算法部分,建议大家找算法书籍再去阅读。
算法的特性
输入输出、有穷性、确定性、可行性
算法设计的要求
正确性、可读性、健壮性、时间效率高和存储量低
其中正确性中有提到四个层次,我们除了需要处理正确路径外,尤其要注意的是
- 算法程序对于非法的输入数据能够得出满足规格说明的结果
- 算法程序对于精心选择的,甚至刁难的测试数据都有满足要求的输出结果。
算法时间复杂度 O(n)
首先根据算法,推导出其命令的执行次数 T(n) 和问题规模 n 的对应关系函数 f(n),然后对 f(n) 进行下列处理:
- 用常数 1 取代运行实践中的所有加法常数;
- 在修改后的运行次数函数中,只保留最高阶项;
- 如果最高阶项存在且不是 1,则去除与这个项相乘的常数。
得到的结果即是算法的时间复杂度 O(n)。大家结合下面的例子,可以更好的理解:
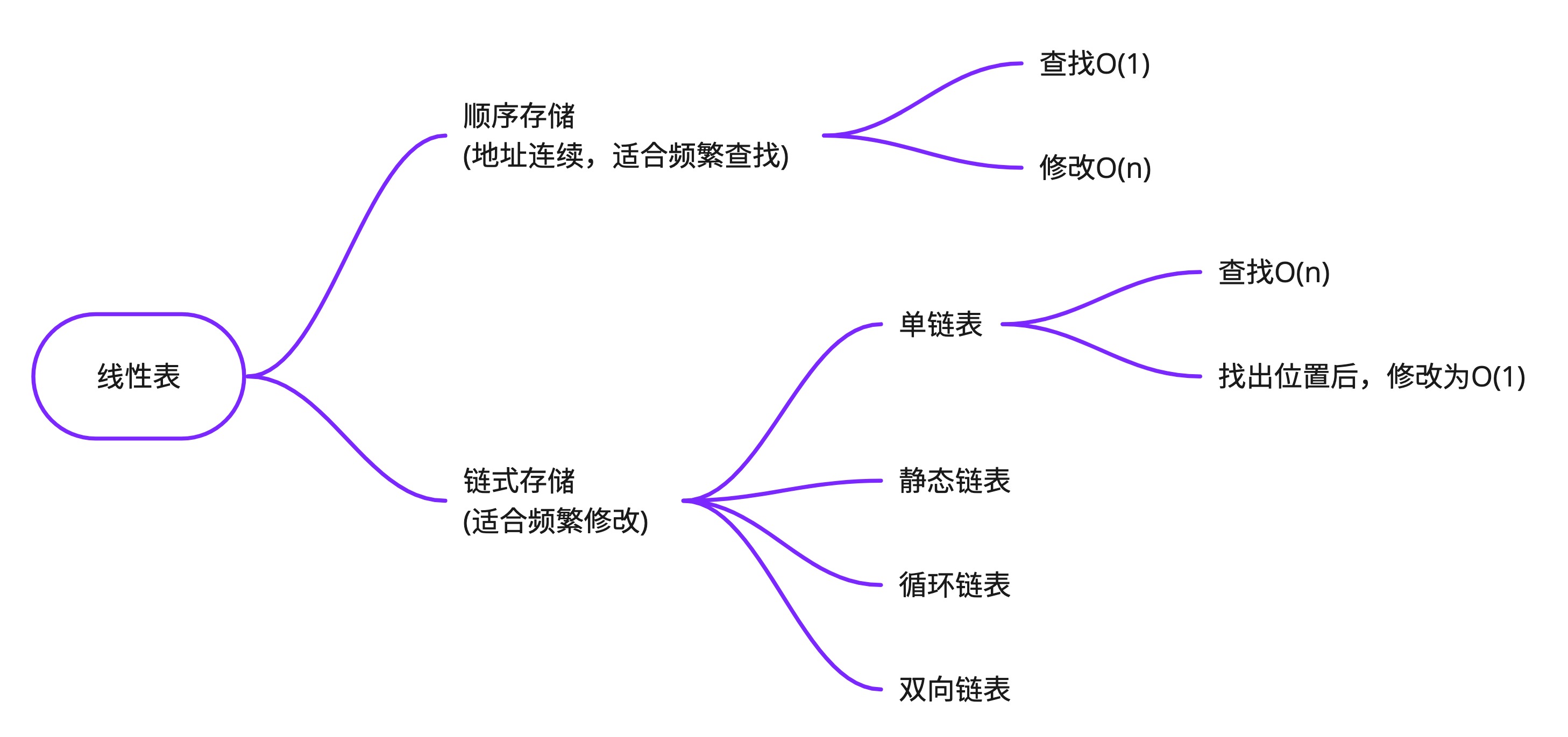
线性表
线性表是零个或多个数据元素的有限序列。
栈
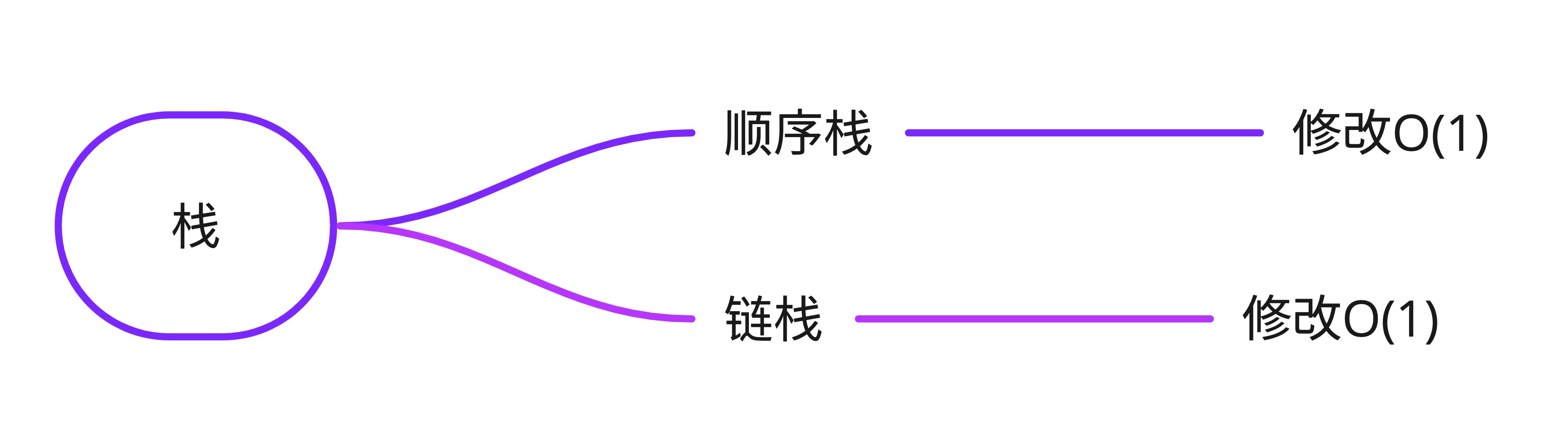
栈是限定仅在表尾进行插入和删除操作的线性表。
后进先出(Last In First Out)是栈最主要的特点。
队列
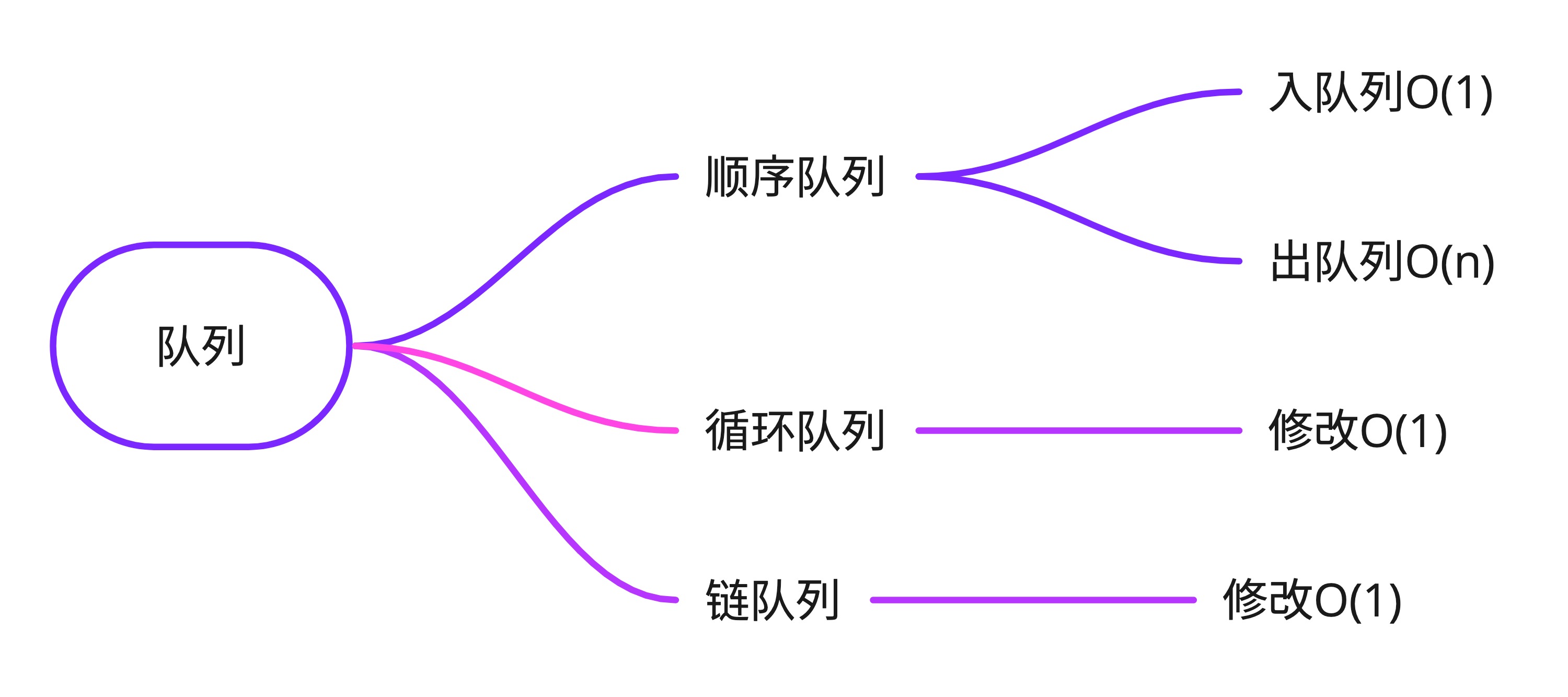
队列是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
先进先出(First In First Out)是队列的特点。
串
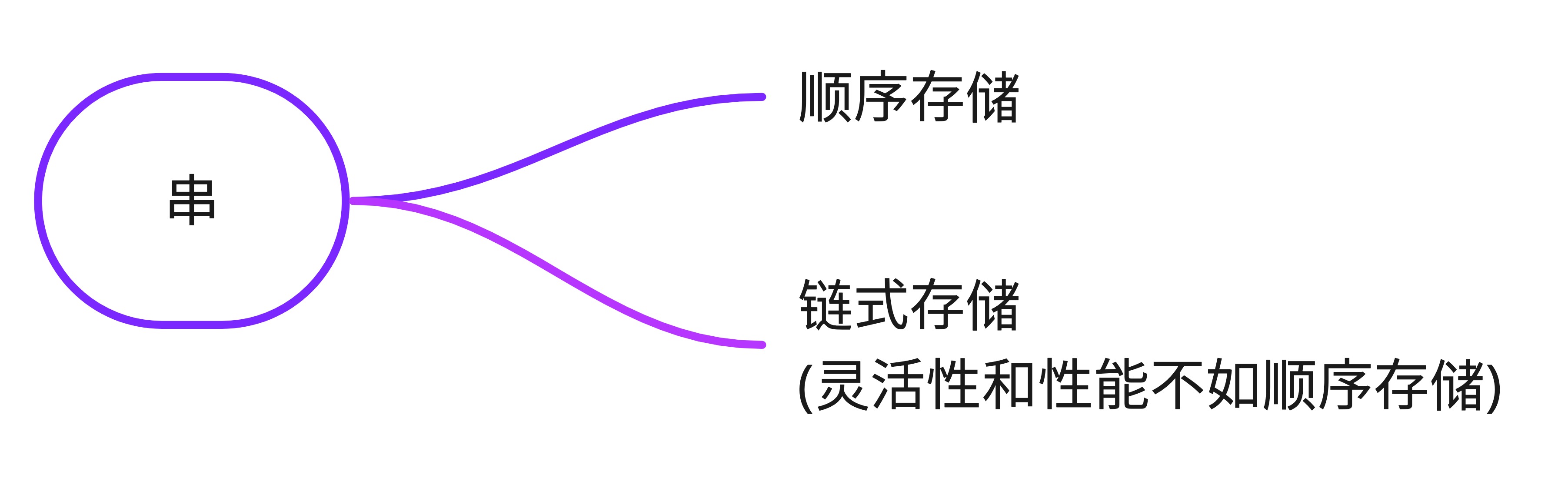
串是由零个或多个字符组成的有限序列,又名字符串。
串本质上是一种线性表的扩展。
树
树是 n (n>=0) 个结点的有限集。
n = 0 时称为空树。
在任意一颗非空树中:1. 有且仅有一个特定的称为根的结点;2. 当 n > 1 时,其余结点可分为 m (m > 0) 个互不相交的有限集,其中每一个集合本身又是一棵树,并且称为根的子树。
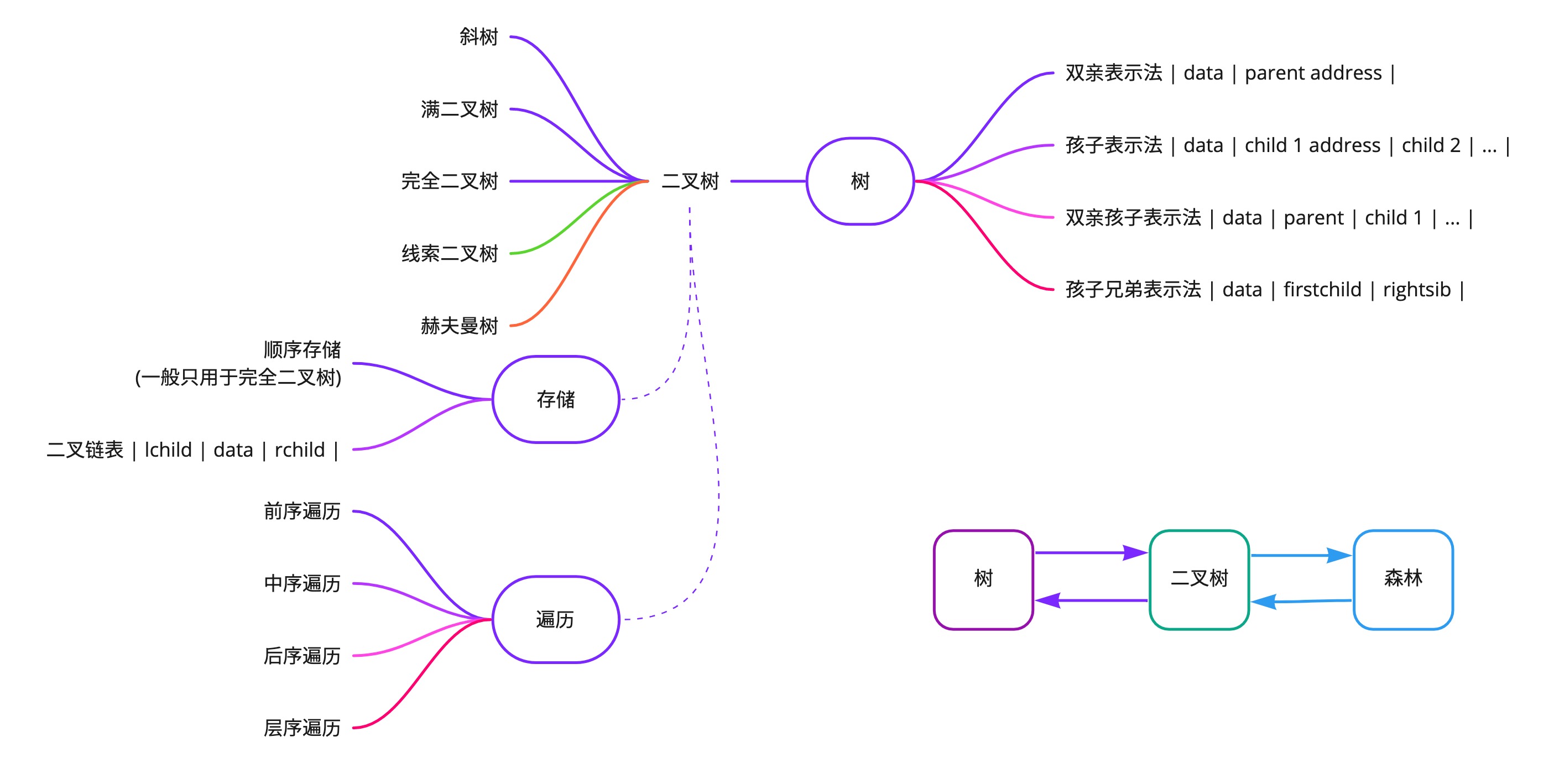
树的概念和术语比较多,其中比较重要的是二叉树的遍历。
遍历二叉树
前序遍历
对于非空二叉树,先访问根结点,然后前序遍历左子树,再前序遍历右子树。
中序遍历
对于非空二叉树,从根结点开始(并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。
后序遍历
对于非空二叉树,从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点。
层序遍历
对于非空二叉树,从树的第一层(也就是根结点)开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。
图
图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中 G 表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合。
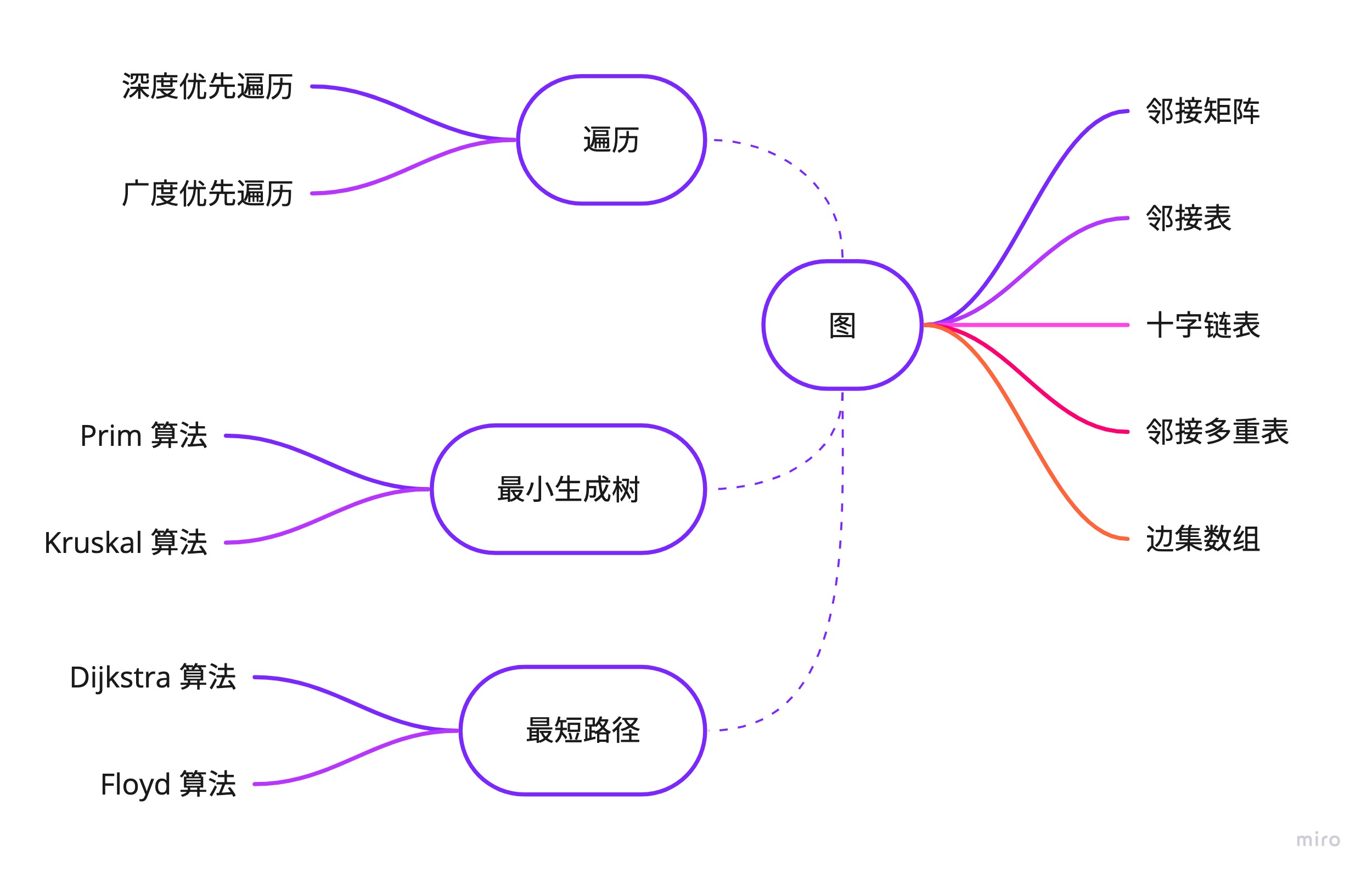
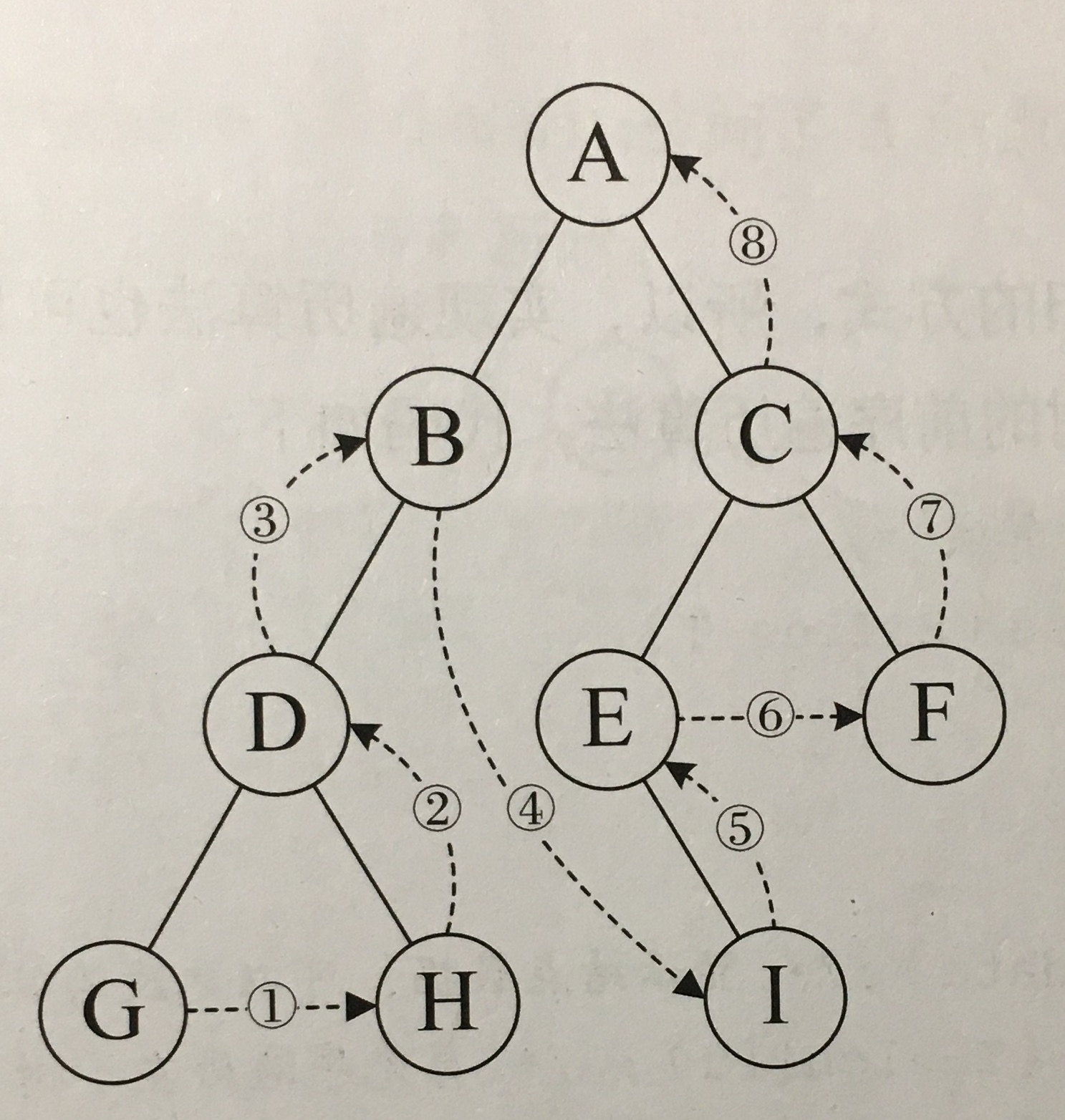
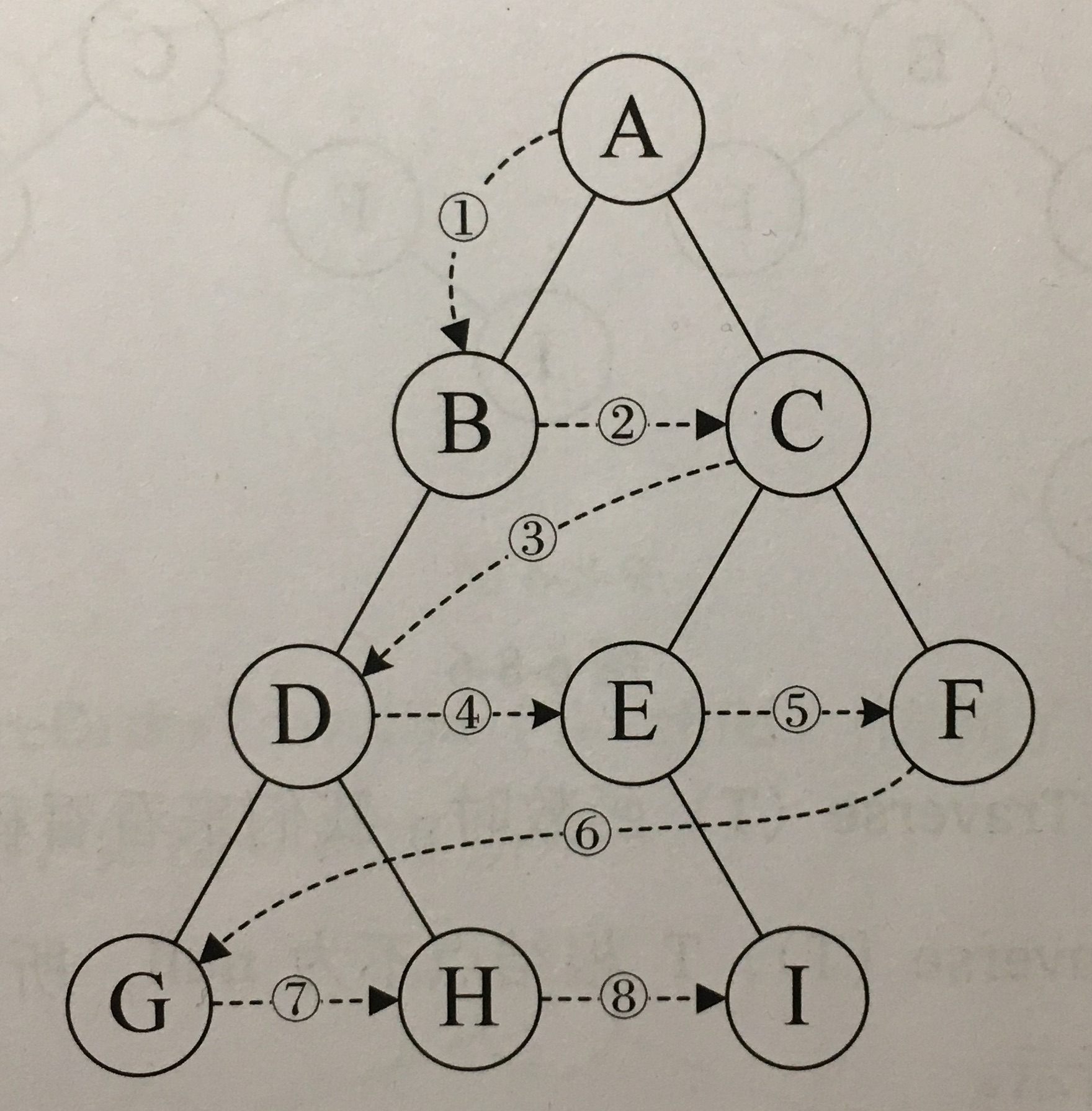
图的深度优先遍历类似于树的前序遍历,广度优先遍历类似于树的层序遍历。两种遍历在时间复杂度上是一样的,所以它们在全图遍历上没有优劣之分,深度优先更适合目标比较明确,以找到目标为主要目的的情况,而广度优先更适合在不断扩大遍历范围时找到相对最优解的情况。
算法图解
了解了数据结构,就能更好的学习和理解各种算法,等看完《算法图解》一书之后,再写一篇读书笔记加以总结。


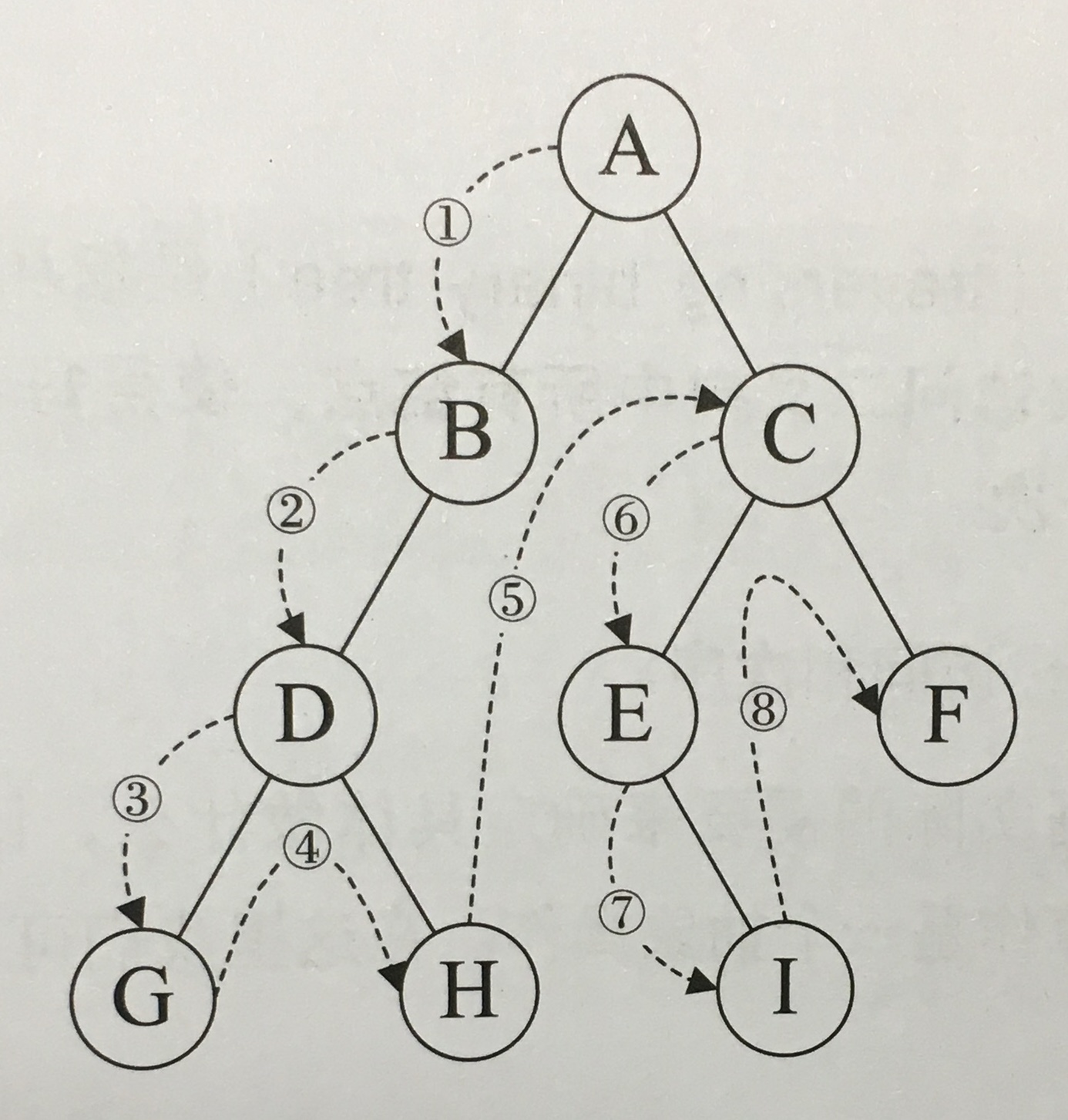
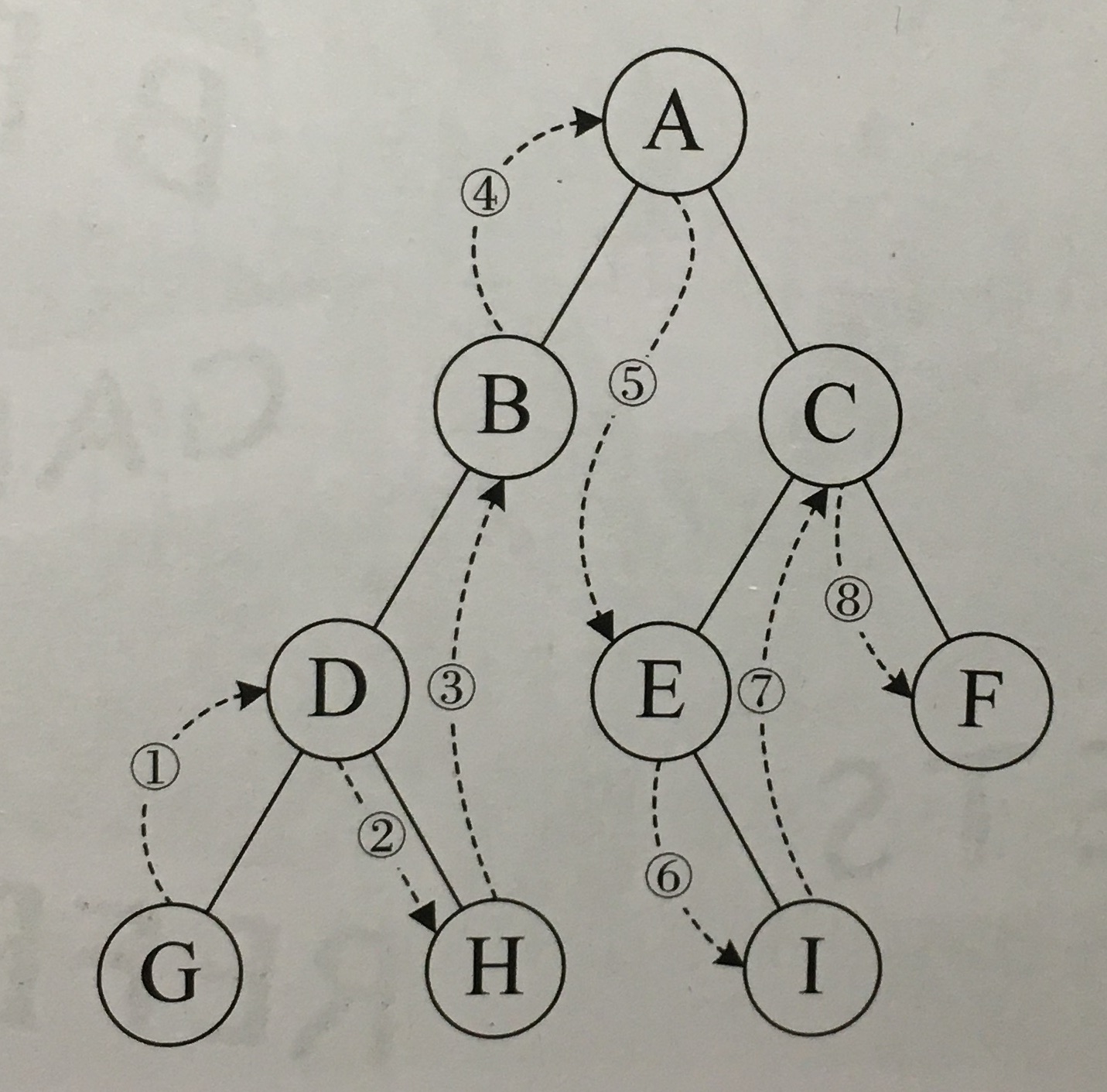
Comments powered by Disqus.